三次函数的性质 -k8凯发平台

三次函数的性质

形如f(x)=ax³ bx² cx d(a≠0)的函数，被称为“三次函数”，则它的性质如下：

定义域：x∈r

值域：y∈r

三次函数的值域求解，可以借助极限的思想，根据函数的表达式可知，影响其值域范围的主要是“ax³”这一项，因此可得：

当a＞0时，x趋近于 ∞，则f(x)趋近于 ∞；x趋近于-∞，则f(x)趋近于-∞。

当a＜0时，x趋近于 ∞，则f(x)趋近于-∞；x趋近于-∞，则f(x)趋近于 ∞。

又因为f(x)是连续的函数，且x∈r，所以f(x)的值域为r。

备注：由于三次函数的值域为r，则它的函数图像与x轴至少有一个交点，换句话说三次方程至少有一个根。

一、图像和单调性

f(x)=ax³ bx² cx d, (a≠0)

∴f'(x)=3ax² 2bx c

则△=(2b)²-4∙3a∙c=4(b²-3ac)

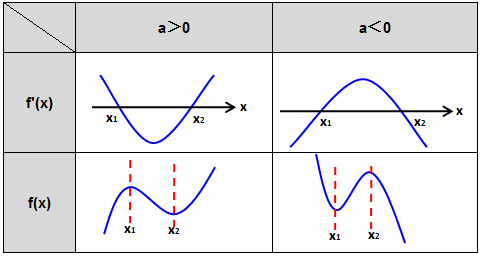
1.当△＞0，即b²-3ac＞0；

f'(x)有两个不同的根，即f(x)有两个极值点x1、x2(令x1＜x2)，则三次函数单调性的情况如下：

当a＞0，f(x)在(-∞，x1)，(x2， ∞)为单调递增，(x1，x2)为单调递减；

当a＜0，f(x)在(-∞，x1)，(x2， ∞)为单调递减，(x1，x2)为单调递增。

则f'(x)、f(x)大致图像分布如下：

2.当△=0，即b²-3ac=0；

f’(x)只有一个根x0，无极值点，则三次函数单调性的情况如下：

当a＞0，f(x)在r上为单调递增；

当a＜0，f(x)在r上为单调递减。

则f’(x)、f(x)大致图像分布如下：

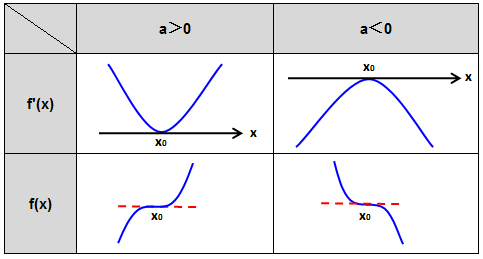
备注：由上图表可知，f(x)为单调函数，且点(x0，f(x0))是函数f(x)的一个拐点。拐点的定义：在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点(即曲线的凹凸分界点)，另外拐点的二阶导数为零，而三阶导不为零。

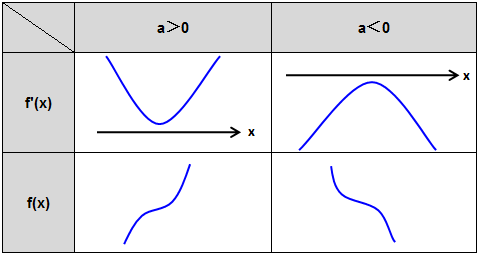
3.△＜0，即b²-3ac＜0；

f’(x)无实根，无极值点，则三次函数单调性的情况如下：

当a＞0，f(x)在r上为单调递增；

当a＜0，f(x)在r上为单调递减。

则f’(x)、f(x)大致图像分布如下(无拐点)：

二、极值与最值 

由函数的图像可知，三次函数的极值与最值的情况如下：

①当△＞0，即b²-3ac＞0；函数有极值，且极大值和极小值点各1个，无最大值和最小值点。

②当△≤0时，即b²-3ac≤0；函数无极大值和极小值点，也无最大值和最小值点。

三、方程根的分布

对于讨论ax³ bx² cx d=0的根的分布情况，在研究函数的图像部分可知，f' (x)的判别式△对f(x)的极值点的个数有影响。

1.当△＞0时，即b²-3ac＞0；

此时f(x)有两个极值点x1，x2

(1)当f(x1)∙f(x2)＞0时，此时方程只有1个根(函数图像与x轴只有1个交点)，具体如下图所示：

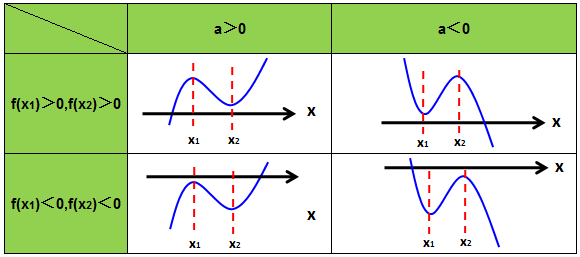
(2)当f(x1)∙f(x2)=0时，此时方程有2个根(函数图像与x轴有2个交点)，具体如下图所示：

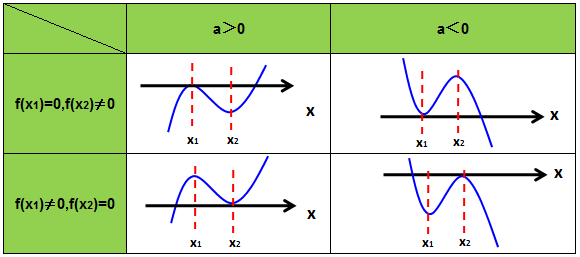
(3) 当f(x1)∙f(x2)＜0时，此时方程有3个根(函数图像与x轴有3个交点)，具体如下图所示：

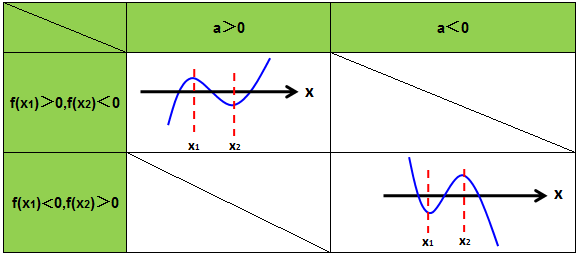
2.当△≤0时，即b²-3ac≤0；

由函数的单调性可知，此时f(x)恒为单调函数，只与x轴有一个交点，即方程只有一个根。

综上可知，三次方程最少有一个根，最多有三个根。

四、三次方程韦达定理

设三次方程ax3 bx2 cx d=0(a≠0)的三个根分别为x1，x2，x3，则韦达定理为：

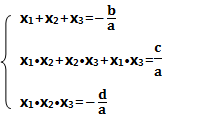
备注：如果三次方程只有1个或者2个根的情况，上述的韦达定理依然成立。另外在高考中对于三次方程的求解要求不是很高，求解的根值也相对简单，通常为整数，在求解过程中如果能够结合三次方程的韦达定理，那题目做起来就更得心应手了。

五、对称中心  

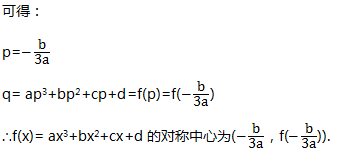
六、奇偶性  

对于函数f(x)= ax³ bx² cx d(a≠0)，只有当b=0且d=0时，f(x)为奇函数，否则f(x)无奇偶性。

七、函数切线 

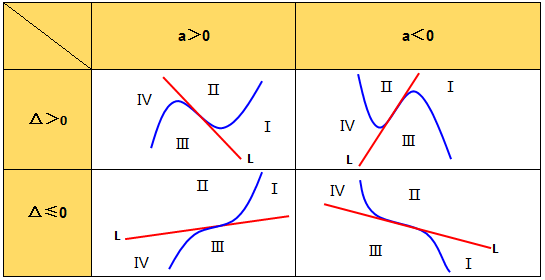
如下图的表格汇总可知，过三次函数f(x)图像的对称中心做切线l，则坐标平面被函数f(x)和切线l的图像分割为四个区域，有如下结论：

(1). 过区域ⅰ , ⅳ的任意点作f(x)的切线，有且仅有3条；

(2). 过区域ⅱ ，ⅲ的任意点以及对称中心作f(x)的切线，有且仅有1条；

(3). 过切线l上或f(x)图像上的任意点(对称中心除外)作f(x)的切线，有且仅有2条。

感谢微信公众号：高中数学王晖